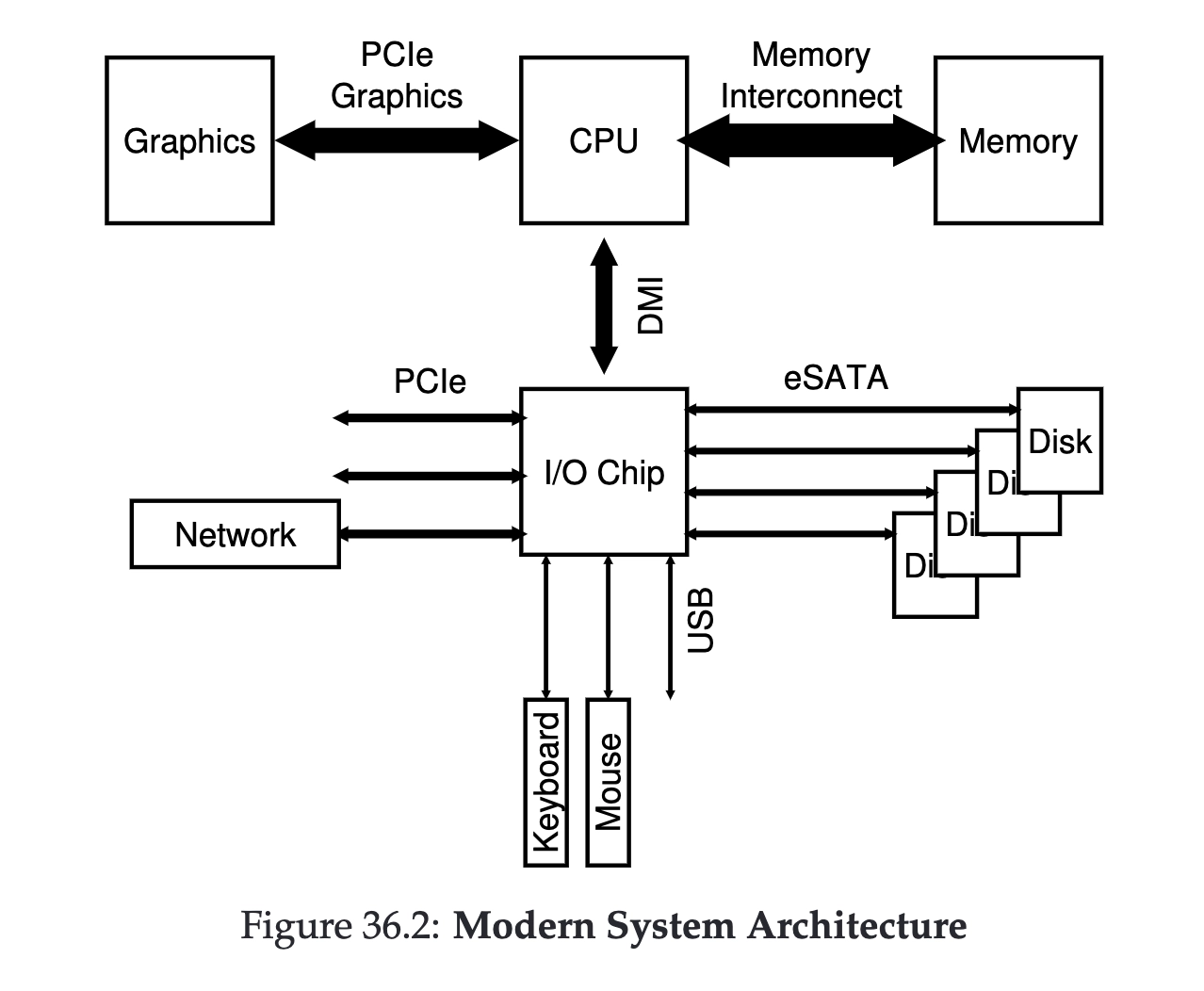
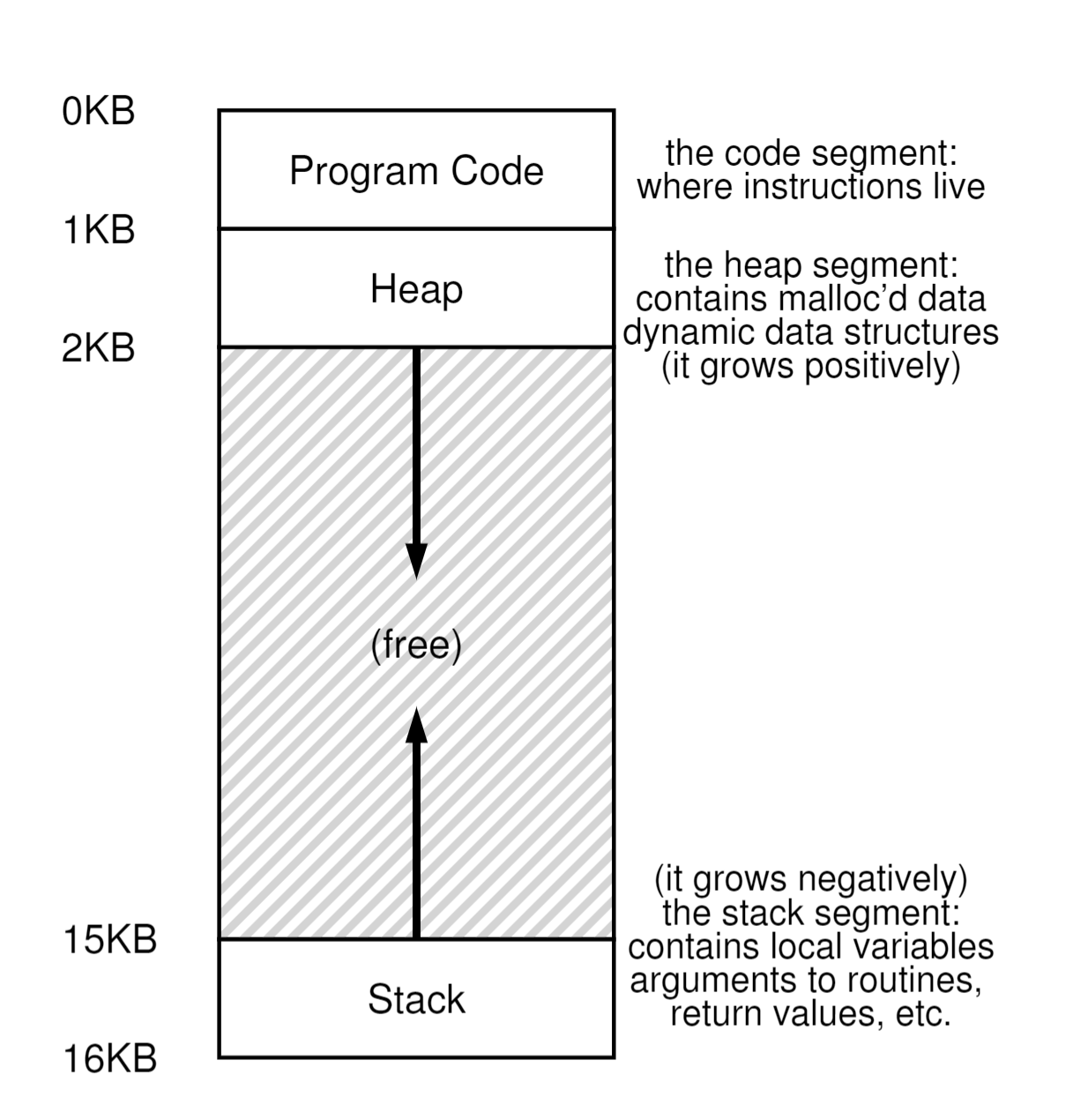
这章如名字,主要讲的是磁盘冗余阵列,也就是我们常说的RAID。一种扩展磁盘的容量、提升磁盘可靠性的技术。
RAID存在RAID0到RAID6等多种方案。评估一个RAID方案,主要从容量、可靠性、性能这三个方面。RAID的特点和前面的一些虚拟化一样,将多个磁盘虚拟化为一个磁盘,来对上游提供服务。
RAID 0 条带化分块
RAID0是最基础的思路,实现的功能也很简单,对多个磁盘进行合并。他使用了条带化(stripe)的方式来对多个硬盘进行分段以及分块,将多个磁盘组合并按次序进行标记分段,然后存储数据时只要使用对应分段即可。

可以看到,跨越4个磁盘,我们通过分段让他们依旧有了连续性关系,所以我们就可以像操作一个磁盘那样操作4个磁盘了。
这里会有一个关键的权衡:如何选择每段的大小?首先注意一点,不同物理磁盘是可以并发读写的。所以,段分段过小时,我们可以拥有更好的并发性,但是会过多的跨越磁盘读取数据。段分段过大时,我们读取大文件会有更好的连续性,但是也会因为丧失并发性而失去一部分性能,并且性能此时就纯依赖于一个磁盘的性能了。
一个极端的例子可以说明这个情况:当我们的一个段时4kb时,此时读取一个16kb的文件,刚好是0-3四个分段。在4个磁盘并发读取的情况下,性能可以是接近4倍(因为还需要将数据合并,会有一定开销)。
评估RAID 0
我们评估磁盘的性能与之前一样,分别要考虑2个场景:顺序、随机。
给定单个磁盘的性能,我们来进行一下计算单个磁盘的S和R,其中S表示顺序sequential,R表示随机random。
Average seek time 7 ms
Average rotational delay 3 ms
Transfer rate of disk 50 MB/s
$S=\frac{Amount of Data}{Time to access}=\frac{10MB}{210ms}= 47.62MB/s$
$R=\frac{Amount of Data}{Time to access}=\frac{10MB}{10.195ms}= 0.981MB/s$
从吞吐量的角度看性能(多磁盘间可以并发读写)。在整个RAID0下,访问整个RAID0和访问单个磁盘的延迟大致相同,所以RAID0的实际S=N·S,R=N·R, 基本是线性的提升。
所以我们总结下RAID0表现:
容量:线性提升,RAID容量=单个磁盘·N
可靠性:0,没有任何可靠性措施
性能:线性提升,RAID性能=单个磁盘·N
RAID 1 镜像
RAID1开始,带上了机制以保证可靠性。

可以看到,通过巧妙的分块,我们对每个分块做了一份冗余。每个分块我们都会保存一份镜像在另外的硬盘上。
评估RAID 1
依旧从3个角度去评估。我们在这里只评估所有数据仅有一份冗余的情况,因为更多份冗余的场景也很容易按照这种方式去计算
容量
很显然,容量的降低取决于我们镜像的数量,在只备份一份的情况下,我们的容量变为了N/2。
可靠性
从可靠性上来看,RAID1最佳情况下可以容忍N/2的故障。即D0和D2都挂了。最差可以容忍1的故障,即D0-D3任意一个挂了。
性能
这里有一点比较特殊,因为我们提到了跨磁盘之间的操作可能是并行的,那么好像读或者写2份在同一个磁盘的数据好像对性能的影响微乎其微?
顺序读
但是其实不是这样,考虑到我们要计算综合吞吐的话,在顺序读时,因为磁盘分块被我们分割开了,哪怕是顺序读,0-1-2-3-4-5-6也可能跨了非常多的磁盘(D0,D2,D0,D2,D0,D2),此时考虑到还有额外2种情况:
- 读取时因为有2份数据,所以可能不只是2个盘,而是D0D1D2D1D3
- 磁盘本身会旋转,本身的顺序读被完全割裂了
所以顺序读的实际吞吐可能接近$(\frac{N}{2}·S) MB/s$
顺序写
顺序写也是一样,因为要保证2份数据同时写完才算写成功,即使可以并发写,但是会带来另一个磁盘可能刚好错过扇区的成本,所以顺序写的吞吐也是$(\frac{N}{2}·S) MB/s$
随机
随机读反而不受影响,因为本来就要承担该承担的一切,所以还是N·R
随机写于顺序写一样,也是$(\frac{N}{2}·R) MB/s$
ps:这里文中的计算看看大概思路了解需要考虑那些额外因素就好,实际现实上不能这么算,加深对磁盘运作机制的理解就可以
RAID 4 通过奇偶校验节省空间
RAID4是一种优化,通过奇偶校验节省副本所需要的空间

奇偶校验可以使用一个额外的盘上的分块,来存储前面一系列分块的奇偶校验和,以此来节省空间。
奇偶校验保存方式
- 对于同一行的分块,都在Disk4上有一个额外的分块,来保存奇偶校验值
- 奇偶校验值保存了前面D0-D3中对应分段的每一个bit位的奇偶校验值
奇偶校验位的含义以及计算
-
奇偶校验位为0或1
-
奇偶校验位与它所对应的bit,1的数量必须是偶数
-
快速计算的话,只需要对前面的位整个进行异或XOR,得到的就是奇偶校验位,比如下图,0^0^1^1=0,0^0^1^0=1
| Disk0 | Disk1 | Disk2 | Disk3 | Disk4(奇偶校验bit) |
| ----- | ----- | ----- | ----- | :------------------- |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 |
奇偶校验位如何做到冗余
- 奇偶校验位可以完成1个盘损坏情况下的冗余,可以认为是1档冗余
- 因为奇偶校验位的特性(奇偶校验位bit与所有数据bit中1的数量必须为偶数),所以我们可以简单的拥有以下恢复策略当某个盘不可读取时,再次检查整行的值
- 如果此时1的数量为奇数,说明丢失的那bit是1
- 相反,如果此时1的数量还是为偶数,那么说明丢失的那bit是0
评估RAID 4
容量
无论多少个磁盘,奇偶校验只需要一个额外磁盘保存奇偶校验位,所以容量是(N−1)·B
可靠性
从原理上来说,奇偶校验位的可靠性最多允许一个disk坏掉
性能
顺序读
顺序读我们可以正常操作除奇偶校验盘外的所有,所以是(N−1)·SMB/s
顺序写
顺序写时,考虑到一种情况:我们可以直接一行一行块的写,即直接从分块0写到分块P0,这个时候直接在写前面的时候也就把奇偶校验计算出来了,所以写的速度也是(N−1)·SMB/s
随机读
随机读与上面类似,所以还是(N-1)·R
随机写
随机写十分复杂,要考虑的点非常多,是一个重点。
首先是如何得到新奇偶校验的值
在写入某个块时,奇偶校验位的值也需要被更新,我们想一下,最基本的更新策略可以是这样:
- 更新某个分块(比如说Disk0上的0)时,更新后,我们读取同一行的所有数值,重新计算奇偶校验并写入P0
但是这显然成本过高了,更新一个分块,反而要读取整行所有的分块吗?考虑到奇偶校验和的来源,我们可以有另一种简单的办法
- 通过这个分块的原值、新写入的值、奇偶校验位的值,来计算新的奇偶校验位——$P_{new}= (C_{old}⊕C_{new})⊕P_{old}$
然后,写入会存在很明显的瓶颈
在随机写场景,当随机写连续发生在2个disk时,按照我们之前的估计,2个disk本身是支持并发一起写的,但是引入奇偶校验后,会出现问题,如下图

我们会发现,及时4和13因为分别位于D0和D1,他们之间可以并发进行写,但是因为他们都需要更新奇偶校验和,所以都需要在D4上去写,D4成为了随机写的瓶颈!
事实上,在这种场景下,整个随机写最终都会成为在D4上的串行写,所以我们随机写的性能,不只达不到N*R,甚至小于了单个磁盘的R,考虑到每次写入奇偶校验位时,都需要先读取原来的校验位来做计算,所以实际随机写的性能大约是$(\frac{R}{2})MB/s$(因为又要读一次又要写一次,所以大概是一半)。
ps:还是那句话,这种算法知道考虑的点就行,实际的值准不准确别过于认真
RAID 5 轮流保存奇偶校验位
RAID5也是一种优化,来优化RAID4的性能瓶颈
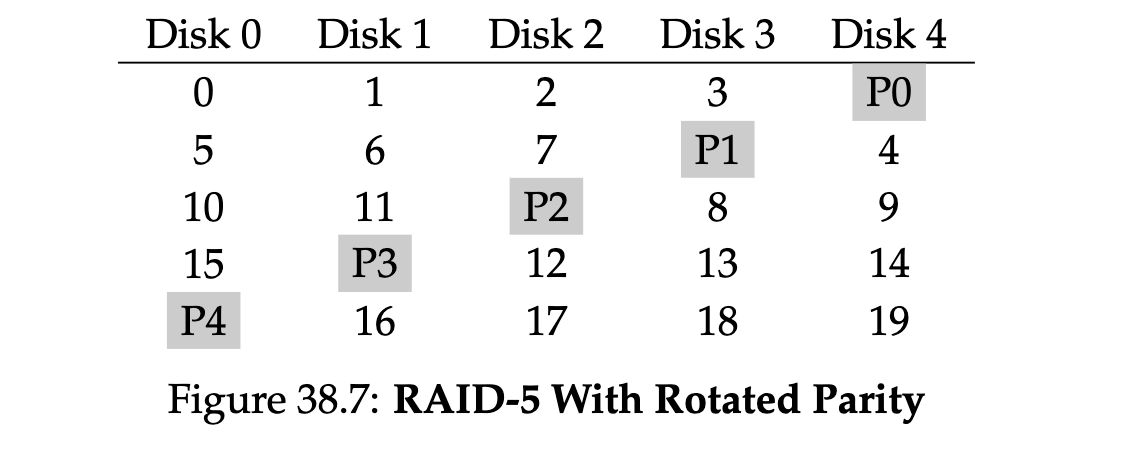
参考这个图,RAID 5不再使用一个固定的盘来保存奇偶校验位,而是每个盘轮流在一行中使用一个分段来保存奇偶校验位。在评估之前,我们首先就可以发现它主要就是规避了RAID4中使用一个盘来做奇偶校验盘的单写问题。
评估RAID 5
容量
与RAID 4一样
可靠性
与RAID 4一样
性能
除了随机写以外,基本都与与RAID 4一样,随机读会稍微好一些,因为我们现在可以读所有磁盘了
随机写
随机写会提升不少性能,因为我们避免了写阻塞在一个盘上的问题,但是因为奇偶校验位会在任意盘上,所以我们在大量随机写时,所有盘都在狂飙(写D0时要写D4的校验,写D4时又要写D0的校验,互相之间都是套娃)。我们预估这种情况下,实际写入的速度估计是$\frac{N}{4}·R$
RAID总结
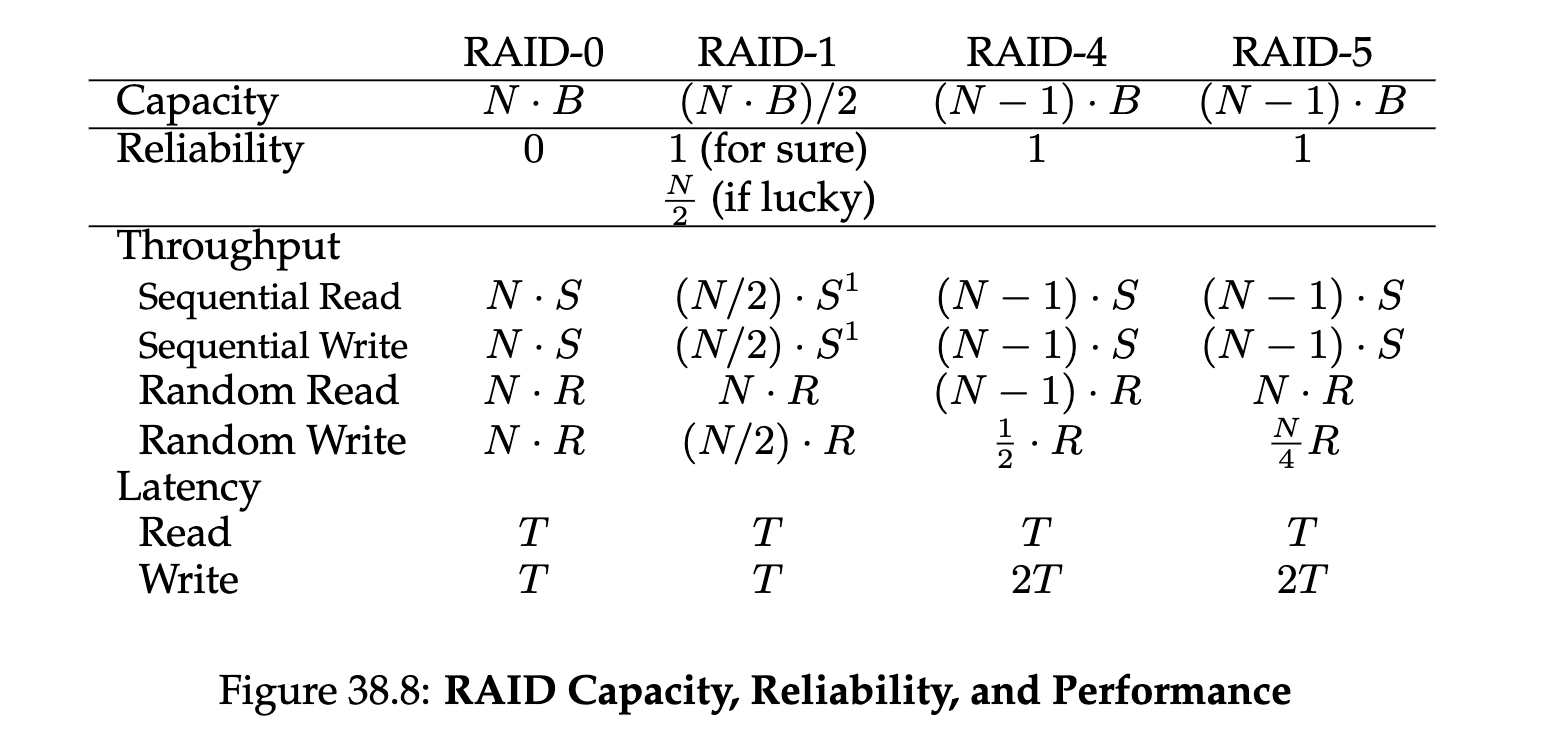
RAID是在软件层(磁盘控制读取写入)做一系列设计,去实现多磁盘的组合使用,其中几个主要方案就是这章中介绍的,其他的RAID2、3、6可以自己再去了解下,但是核心思路都已经在本章中的几个方案里提到了。
RAID方案的取舍也是取决于你对容量、性能、可靠性的权衡取舍。个人感觉对于家里的NAS来说,基本上RAID-5就是最佳方案了。